The following lesson plan was written by Emily Clader and Daniel Reck for STEM to Story: Enthralling and Effective Lesson Plans for Grades 5-8 (Jossey-Bass, 2015), a collection of lesson plans compiled by 826 National, a network of nonprofit organizations dedicated to helping students, ages six through eighteen, with expository and creative writing, and to helping teachers inspire their students to write. This lesson plan is intended for two sessions of two hours each.
We're letting you in on a bit of a secret here: math and writing are pretty much the same thing. This might come as a surprise, but think about it. Like writing, math helps us understand the world by allowing us to describe the rules it follows and explore what would change if we broke those rules. In this lesson, students learn how imposing structure on writing can inspire them even while constraining them. By developing an awareness of mathematical structure in life, they will be able to imagine the world in a different and exciting new way. Together, you'll create infinite poems using fractals, imagine life on a doughnut, and speculate about a universe where time goes crazy. Along the way, everyone will learn some cool math facts and some helpful writing strategies.
In this session, students learn that shapes don't have to be silent, and poetry doesn't have to be linear, as they write shapes in verse, and verse in shapes.
Materials
- Copies of the “Fractal Poetry: A Step-by-Step Guide” handout.
The Lesson Takes Shape (20 minutes)
Start by asking students to share their favorite shape and why they like it. A triangle? A rhombus? Will someone go wild and choose a dodecagon? Once everyone's had a chance to voice his or her polygon preferences, dive into some meatier topics:
- What is math? What does it do, or what is it about? Why do you do math?
- Does math have anything in common with writing? What about creative writing?
After allowing the students to share their ideas on these questions, offer a definition of math, such as the following:
Math is a language in which we can give precise definitions of concepts that would otherwise be hard to pin down.
Multidimensional Math (10 minutes)
Your students probably have some idea of what dimensions are. They know that a sheet of paper is two-dimensional, or that the planet Earth is three-dimensional. (If you have time and access, showing a clip from "Homer3" in the "Treehouse of Horror" episode of season 7 of The Simpsons is a very entertaining way to get the point across.) But what about a collection of dots (or points, mathematically speaking)—does that have a dimension? In the language of math, it's possible to give a definition of dimension. Then, equipped with that definition, we suddenly have the power to make sense of new ideas—we can figure out what dimension that collection of dots has. And we can know what four-dimensional means, or one hundred–dimensional, or even one half–dimensional or infinity-dimensional. (Check out this lesson's “For You to Know” section for some helpful explanations related to this concept, as well as a few other mathematical ideas that come up in the activities.)
When viewed as a language, mathematics becomes a tool both for describing the world and for expanding the scope of our imagination. In this way, it is similar to creative writing. A mathematician, like a writer, uses the familiar as a springboard to conceive of new worlds, and gives those worlds substance by putting them into language.
Zooming In (30 minutes)
In this session, students will learn about a mathematical object known as a fractal. Before you explain exactly what a fractal is, it's helpful to show a few pictures to spark imagination and curiosity. (There are a ton of great images to choose from online; just search for “fractal” and select a handful of eye-catching examples, ideally looking for ones that clearly illustrate the definition.) You can also show students a video. Search online for “fractal zoom,” which will yield some stunning videos of fractals in motion.
Allow the students a moment to try to articulate what these images have in common, or, more simply: What's so cool about these pictures and videos? After a short discussion, define the term:
A fractal is a shape that contains a copy of itself inside of itself. If you zoom in on one part of the shape and keep zooming in, you'll eventually see something that looks just like what you started with.
We've found it's helpful to return to the images while explaining this concept to students, pointing out the smaller copies of the fractal inside the larger shape. There are even examples of fractals in nature, like Romanesco broccoli, where each floret is made up of smaller florets that each look like a whole piece of broccoli. Some simple fractals, like the Sierpinski triangle or the Koch snowflake, are easy to draw on your own. (We highly recommend that you have students try to draw one or the other; there are instructions in the “For You to Know” section of this lesson, so you can teach the students how to draw them if time and interest permit.)
We've come up with a simple method for turning any shape into a fractal. It will take students fifteen minutes the first time, give or take.
Here's the method:
1. Draw a simple shape.
2. Pick any two points on the perimeter of the shape. Label one of the two points with an X and the other point with an O.
3. Draw a smaller copy of the shape (about half the size of the original one), with its own X and O in the same places as on the original shape. But here's the key: draw it so the X on the smaller shape is on top of the O on the original shape. This will probably require you to rotate the smaller shape, but that's good.
4. Draw an even smaller copy of the shape (about half the size of the previous one), with its O on top of the X on the previous shape.
5. Repeat until the shapes get too small to draw.
It's a bit tricky to explain the procedure in words, but an example should make the idea clear:
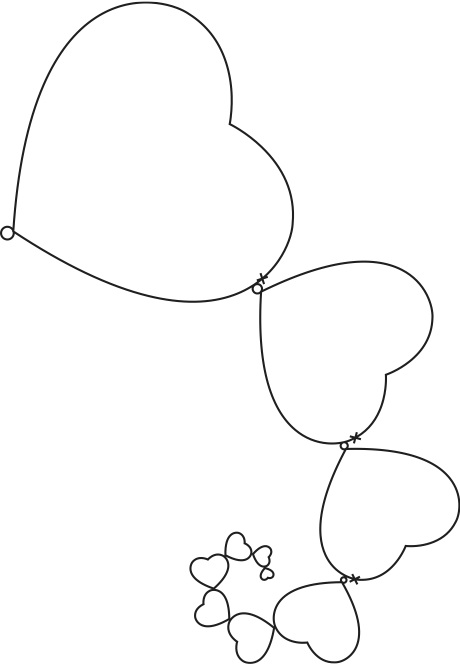
Model the procedure for your students first. Then ask them to try it for themselves with a very simple shape to get the hang of the method. If your students have no problems with triangles, circles, or hearts, see what they can do with smiley faces, airplanes, or trees! Be sure to leave time for sharing.
Putting the Writing in Writing (25 minutes)
So, what do fractals have to do with creative writing? To make the connection, we need to think about the idea of recursion.
Recursion, roughly, is when something feeds back into itself. Fractals are recursive, because when you zoom in you wind up back where you started. There is recursion in some works of art, like M. C. Escher's Drawing Hands, in which one hand is drawing a picture of another hand, which is drawing a picture of the first hand, and so on. Students may have seen images where someone is holding up a picture of him- or herself holding up a picture of him- or herself (and so on). They may also have experienced this phenomenon themselves by standing in front of a mirror with another mirror in their hands. That's recursion, too. Music can be recursive, like “The Song That Never Ends,” which loops back into the beginning whenever it reaches the end. All recursion is in some way infinite, because when something feeds back into itself, it can always keep looping back and back forever.
In this session, students are each going to write a poem that has the same form as “The Song That Never Ends” (but that is, we hope, less annoying); the end of the poem will loop back into the beginning. Here's an example of a recursive poem that a student wrote in a previous version of this lesson:
Always Dreaming
A person is always dreaming
about a cool dude that
is himself because he
wants to be cool
so he keeps on dreaming
of
A person is always dreaming
about a cool dude that
is himself because he
wants to be cool
so he keeps on dreaming
of
—Harrison Li, age eleven, Michigan
Distribute the “Fractal Poetry: A Step-by-Step Guide” handout and challenge students to write their own recursive poem. Tell them not to worry about the length; even if it's only five or six lines long, when it loops back on itself, it will become infinite! The only important thing is that the ending gives a way to go back to the beginning.
There are a couple of ways students can do this. Much like “The Song That Never Ends,” their poem can end with an incomplete phrase like “because … (This is the song that never ends)” or “I say … (My name is Yon Yonson).” A similar option is ending the poem with a question (“What is your favorite color?”) and starting it with the answer (“The color blue”).
For even more wordplay, have students write an acrostic—a poem where the first letters of each line spell out a word—and have that word start or end the poem. Here's an example:
Cat
Can't stand it anymore
All I want to do is get away from
That …
Encourage students to experiment here. Can they come up with new structures for recursive poems? Have them try different things and find something that they like. Again, it doesn't have to be all that long.
Get That Writing in (a) Shape (20 minutes)
With the rest of the handout, you can show your students how to turn their recursive poem into a fractal. First (step 2 on the handout), they pick a shape related to the theme or idea of their poem. This is going to be the basis for a fractal. They'll need to draw it a lot of times, so they shouldn't be afraid to keep it very simple. (Of course, don't discourage ambition.) Students can use the back of the handout or a piece of scratch paper to practice drawing their shape until they've figured out something they like and can draw easily.
For step 3, students should find a way to arrange their poem inside the shape. It can go through the inside or around the edge, in lines or in crazy loops. Here's how a poem might look if it were arranged inside a speech bubble, as imagined by 826michigan student Angela Zhang, age eleven, in her poem “Once Upon a Time”:
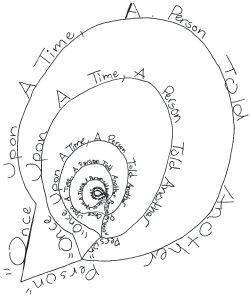
Finally (step 4 on the handout), students make their shape and poetry into a fractal! To do this, they'll use the procedure you practiced together earlier. First, they will mark the spot where the poem begins with an O and the spot where the poem ends with an X. Then, as before, they will make smaller and smaller copies of the shape, with the O of each new copy sitting on top of the X of the previous copy. In each shape, they will write their poem, so the end of the poem on one shape flows directly into the beginning of the poem on the next shape.
From Beginning to End and Back Again (15 minutes)
At the very end of the session, ask everyone to share and marvel at the results.
In this session, students will use ideas from mathematics to imagine and write about worlds in which space and time behave strangely. The first half of the session will be devoted to space, leaving the second half to think about time.
Materials
- Modeling clay or the like
- Foil
- Copies of the “Leaving Space and Time” handout
- String, pipe cleaners, or long strips of paper
Introduction: Playing with Shapes (30 minutes)
For playing with space, the most important mathematical tool is the subject of geometry. Once again, start the class by asking students to share their opinions. Ask them:
- What is geometry?
- If you think geometry has something to do with shapes … what's a shape?
These are hard questions with no single right answer, but one combined definition might be as follows:
A shape is a collection of points in space, and geometry is the study of properties of shapes.
For example, some common properties of shapes that a geometer (a mathematician who studies geometry) might study are length, area, angle, and dimension.
Mathematicians sometimes talk about shapes as abstract things, like “a circle of radius 2” and describe their properties without having any particular circle in front of them. But you can also think about the geometry of the world around you: What is the geometry of our world like?
To get students started, you might note that Earth is a sphere (roughly, but with mountains and valleys). Ask students to think about some of the specifics of this geometry, such as the size of that sphere (very big), and the dimension of the space we move around in (three, but stuck to a two-dimensional ground). They might even notice the fact that Earth is a finite thing, whereas outer space might very well go on and on forever.
There are many stories about characters who live in worlds whose geometry is very different from that of our own. Putting a character in a different sort of space is a way to present him or her with challenges (and sometimes, opportunities) that would not occur on Earth. In Antoine de Saint-Exupéry's The Little Prince, for example, we learn of a boy who lives on a very small planet, who worries that a few trees will overtake the entire surface of his world.
Size is actually a minor difference in geometry; there are much bigger ones. To get students thinking about different geometries, give them some modeling clay, and have them make a planet in a fun shape. Let them know that some of the craziest math is in the field of topology—a cousin of geometry. In topology, a circle and a square are the same thing because, roughly speaking, you can stretch and bend one into the shape of the other. However, a doughnut (mathematically called a torus) is not the same as a ball; you would have to squish the hole in the middle of the doughnut, and that's not allowed. Topologically you can bend and stretch one shape into another, but you're not allowed to close holes or cut out new ones. (Remember from the first session that definitions and rules are important!) Ask your students if they can stretch their shape into a ball—if so, topologically it's the same as the planet Earth. Challenge your students to create a shape that's topologically different from a ball, and then as many topologically different shapes as they can!
Edwin Abbott Abbott's Flatland offers another classic example of interesting geometry; this late-nineteenth-century novella describes a two-dimensional world where the inhabitants are all objects like lines and triangles and squares. Among the many difficulties faced by these two-dimensional inhabitants is the challenge of recognizing each other from afar, because any two-dimensional object looks just like a line segment when viewed head-on.
After they wrestle with that for a bit, bring up Vi Hart's Wind and Mr. Ug. Ask your students what's going on! (The quick answer is that Wind is Mr. Ug! Wind is on a Möbius strip, a special shape that has only one side.) It's fine if they don't understand; let their curiosity and wonder linger. If they do understand that they're seeing a Möbius strip, you can let them know that there's another crazy shape with only one side, the Klein bottle. It can only exist in four dimensions, and its inside is also its outside!
We've discussed a number of examples of weird geometry in fiction, but there's another great source of interesting geometries: video games. The Mario games have some awesome geometry; Super Mario Bros. and many of its sequels are great two-dimensional fun, and Super Mario Galaxy and Super Mario 3D World have amazing three-dimensional mechanics. (Super Paper Mario actually requires switching between 2-D and 3-D views of the world; if you can show a video of this, it's a really great example of how geometry and perspective are connected.) The game Portal shows you what might happen if jumping through one point in space suddenly put you at a different point somewhere entirely different. Ask students if they can think of other examples of video games (or examples from fiction that were missed earlier) in which geometry works differently from the way it does in our world.
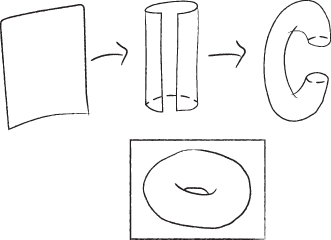
Speaking of video games, here's a fun fact students may not have known: Pac-Man actually lives on a cylinder rather than a square. To see why, remember that when Pac-Man moves off the left side of the screen, he reappears on the right side, and vice versa. This suggests that his world operates as though its left side and its right side were glued together. A square with its left and right sides glued together, though, is nothing but a cylinder. The same kind of reasoning explains the shape of Asteroids, an arcade game that takes place on a doughnut. In that game, moving off the left side of the screen makes you reappear on the right side, but also, moving off the top of the screen makes you reappear at the bottom. So the world of Asteroids is a square with its left and right sides glued together and its top and bottom glued together. Try that for yourself (with a very flexible piece of paper or a piece of tinfoil) and you'll see that you get a doughnut-shaped world.
Shaping the World (20 minutes)
With this perspective in mind, it's time to start writing. Today, students are going to generate an idea for a story that takes place in a world with different geometry from that of our own. Geometry, in their stories, should be more than just a setting; it should be a source of conflict, presenting obstacles or opportunities to the characters that they wouldn't encounter in our world. (If it helps them think about geometry, let students manipulate modeling clay and foil.)
To come up with ideas, it can be helpful to think more about the aspects of our own world that we take for granted.
- How does the shape of the planet Earth affect how we live?
- What about its size?
As a group, you can try to answer these questions, and also to imagine how you might live if Earth's shape or size (or dimension, or some other property) were different. You may also want to keep in mind that the same world can look drastically different depending on your point of view:
- How might a shape look different from the perspective of someone living on that shape, as opposed to someone looking on from the outside? In Abbott's Flatland, for example, the inhabitants see each other as line segments, but an outsider looking on from above sees full shapes. If you showed students Super Paper Mario in action, it helps a lot here!
Even the planet Earth demonstrates this idea of perspective; it took a long time for humans to realize they were living on a sphere, because a sphere this big looks just like a flat surface to a person walking around on it.
Equipped with these ideas to get them started, students should fill out the first part of the “Leaving Space and Time” handout to help them start thinking of a premise for a story that takes place in a world unlike ours.
Transitioning to Time (15 minutes)
Now's when things get really interesting. So far, we have been thinking about the space we live in as a three-dimensional space. It has length, width, and height. But what about time? Albert Einstein taught us that time is really just another dimension, the fourth dimension, of the space in which we live. Time works a little differently from other dimensions, though. We cannot move freely in time like we can along other dimensions, but instead our consciousness experiences time as always moving in the same direction at the same pace. Even more weirdly, time is relative: if you and I are moving at different speeds, time will pass differently for me than it does for you. Although you'd need much more time to explain how this works in detail, for interested students—and instructors!—the Wikipedia page on the theory of relativity is very good.
Just like they did with three-dimensional space, students can imagine time working differently than in the linear fashion we're used to. Our favorite examples come from a book of short stories by physicist Alan Lightman called Einstein's Dreams. In one story, called “14 May, 1905,” there is a center at which time stands still. As one approaches this center, time slows down. Characters wishing to stretch out a particular emotional moment move toward the center. However, spending time near the center means that one ages much more slowly than others farther away. This story, and perhaps several others from Einstein's Dreams, are worth reading if you have the time. Ask the class, “Can you think of other examples of stories that play with time?”
If students struggle to come up with examples, a whole host of stories they probably know involve time travel. Here are a few examples we like:
- Back to the Future
- Time Turners in the Harry Potter series
- The Time Machine, by H.G. Wells
- A Wrinkle in Time, by Madeleine L'Engle
- Groundhog Day
Another example a lot of students will know is the ability of the character Titan Kronos to manipulate time in Rick Riordan's Percy Jackson and the Olympians series. Kronos can slow down time to help him defeat his enemies. Being on the receiving end of this is very confusing. If you were slowed down by Kronos's powers, would you feel like you were moving in slow motion or like things around you were moving unnaturally quickly? Have your students ever been in situations where they felt like time was slowing down or speeding up, for themselves or for the world around them? For example, have any students felt like they suddenly slowed down when they passed a train or bus travelling in the same direction going almost the same speed as they were? What other examples can they think of?
Time permitting, if your students are really into video games, you can bring up examples of games with different time rules. Older examples include Chrono Trigger and Zelda games like Ocarina of Time and Majora's Mask; recent indie games include Braid and Super Time Force. (Interestingly, among other time mechanics, Braid has location-based time-slowing mechanics similar to those of “14 May, 1905.”) Ask your students if they're familiar with any video games in which time plays a role. What do these time powers allow you to do? What problems do they cause, and what are their limitations?
Time to Brainstorm (20 minutes)
Now we are ready to experiment with changing the rules of the fourth dimension of our world. The second part of the “Leaving Space and Time” handout guides students to think about time in new ways, inspiring a premise for a story.
If it helps students brainstorm, have them use a piece of string, a pipe cleaner, or a long strip of paper to create a simple time line. Then have them twist the string or paper around, maybe tangling things up in a knot or two. How would the time line be affected if different events collided?
Time and Space to Write and Reflect (35 minutes)
Now, ask students to pick one or both of the two ideas generated earlier on their handout, about a different kind of space or time, and flesh out as much of a story as possible, using the third part of the handout. Try to save enough time—five or ten minutes—to allow a few of your students to share some of their work aloud.
To end, after students have shared, conclude the lesson by revisiting the question with which the lesson began, What is math? Ask students whether their answer to this question changed over the course of the two sessions.
We think math is awesome. Students often think of math as a collection of facts and methods for solving math problems. Formulas are extremely important for you to be able to understand and use, but there's so much more to math! The formulas and methods students learn in class have not always been known by human beings. They are the fruits of countless hours of labor by people trying to figure out how the world works, in many cases thousands of years ago. These people imagined the world in tons of different ways until they stumbled on the right rules to describe it (and many other worlds besides). And mathematicians are still learning more all the time!
By studying math, we can learn to think logically about the world, to use reason and imagination to understand something in a completely original way. How cool is that?
FOR YOU TO KNOW (AND YOUR STUDENTS TO DISCOVER)
Here is some more information on a few of the mathematical ideas that arise in the lesson, in case you'd like to know more before discussing them with students.
Dimension
Dimension, roughly, refers to the number of degrees of freedom one has when moving about a geometric object. For example, a flat plane is two-dimensional because motion on it can occur in two basic directions: horizontally or vertically. The space we live in, in contrast, is three-dimensional because motion can occur forward and backward, left and right, or up and down. A four-dimensional universe would be one in which movement was possible in four different directions, which, of course, is nearly impossible to visualize.
It is slightly more difficult to understand the dimension of a geometric object that isn't as basic as the two- or three-dimensional spaces we're familiar with, but the trick is to imagine the perspective of a tiny person living on the object. When viewed up close in this way, almost any shape you can think of looks very simple. The surface of a sphere, for instance, is a two-dimensional object. To see why this is the case, pretend you are a tiny person living on the sphere; that shouldn't be hard, because we live on a very big sphere ourselves: Earth. From your point of view on the sphere, it looks just like a flat plane, and this is why we consider the sphere to be two-dimensional. For another example, a squiggly line is one-dimensional, because it looks just like a regular old straight line from the perspective of a really small person standing on it.
Using these ideas, one can make sense of what a four-dimensional or five-dimensional or hundred-dimensional object might look like, but what would it mean to say the dimension of a shape is something weird like ? Fractals have fractional dimension. To see why, we'll need to think of dimension a bit differently.
Dimension dictates how the size of a shape changes when its side length doubles. Consider, on the one hand, the two-dimensional square. If the square has side length 1, its area is 1, whereas if it has side length 2, its area is 4. That is, doubling the side length yields a square that is four times the size of the original one. Cubes, on the other hand, are three-dimensional, and doubling the side length of a cube gives a new cube that's eight times larger. If you could visualize the four-dimensional analogue of a cube (which is called a tesseract), you'd see that when its side length is doubled, the resulting object is sixteen times the size of what you started with. To summarize in somewhat more mathematical terms: if doubling the side length of an object yields an object 2d times as large, then that object has dimension d.
To see why fractals have fractional dimensions, let's play with a relatively simple one: the Sierpinski triangle (see the first figure in this section). First, draw a triangle of side length 1 and subdivide it into a Sierpinski triangle by the procedure described in the “Fractals” section that follows. Then, do the same, but starting with a triangle with side length 2:
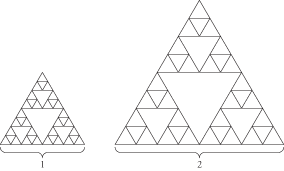
The larger Sierpinski triangle contains three copies of the smaller one. In other words, doubling the side length gives an object three times the size of the original.
This is bizarre, because we would expect the size to increase by a power of 2; remember, if the size increases by a factor of 2d, then the dimension is d. But 3 is a power of 2, it's just a really weird one: you can check on a calculator that 21.58 ≈ 3. The conclusion, then, is that the dimension of the Sierpinski triangle is approximately 1.58.
Fractals
Two examples of fractals that are easy to draw are the Sierpinski triangle and the Koch snowflake. They both have good Wikipedia pages, so you can go there to get a better idea of what they look like.
To draw a Sierpinski triangle, start with a triangle of any size. Subdivide it into a stack of three triangles like so:
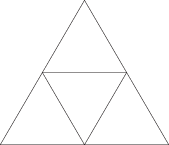
Then, take each of the three triangles in the stack and subdivide them in the same way:
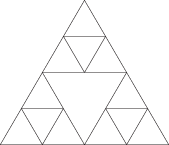
Repeat with each of the nine triangles that result, and so on.
The Koch snowflake also starts with a triangle. In the middle of each of its edges, draw a smaller triangle jutting out:
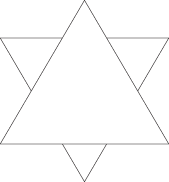
Then draw an even smaller triangle jutting out of each edge of the resulting shape:
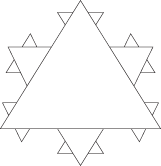
Repeat forever. Which brings us to …
Recursion
As mentioned in the lesson, recursion occurs when something feeds back into itself. An example would be two identical mirrors positioned exactly across from each other, reflecting each other into infinity. Another example would be the box of cocoa that depicts a model holding the same box of cocoa, and so on, and so on. Fractals are also recursive; when you zoom in, you're led back where you started.
Topology
We'll say it: topology is crazy (cool), if a little mind blowing. Topology is similar to geometry, only geometry looks at rigid things (angles, lengths, area, volume, and so on), whereas topology looks at things that can be stretched, twisted, bent, and squeezed—but not torn.
For an example, think of a coffee cup and a doughnut. If you make the cup's handle fatter and its bottom thicker, eventually it would look like a doughnut. And although it would be different in some ways, in others, it would be the same—for instance, it would still have a path, or a “tour,” around the hole in the middle.
On a sphere, any tour that returns to its starting point can be retraced with shorter and shorter ones, until it shrinks to a point. But on the cup/doughnut, the tour around the hole is “noncontractible”—if you try to shorten it, you'll get stuck at some point, when it goes around the hole as tightly as possible.
You can also think of a tour as a closed loop; so a tour on a sphere divides it into a section inside the tour, and a section outside the tour (although you're free to decide which is which!). But the tour around the hole or handle of the cup/doughnut doesn't divide the surface into two parts—you can get from one side to the other without crossing it.
These sorts of things are topological properties: they stay the same as long as we don't cut the object, or punch new holes, or fill an existing hole in all the way.
One of the most important results in recent mathematical history in regard to topology was Grigori Perelman's proof of a nearly century-old problem—the Poincaré conjecture, which is about what three-dimensional shapes are the same as other three-dimensional shapes. The proof involved something called a “Ricci flow with surgery.”
Fun facts aside, it'll be more helpful for you to know a couple of cool world shapes used in science fiction. One of them, which we just discussed, is the torus (doughnut)—it features prominently in Larry Niven's Ringworld and in the Halo series of video games. The other is the Dyson sphere—essentially, the inside of a hollow surface surrounding a star—which was featured perhaps most prominently in an episode of Star Trek: The Next Generation.
The torus is definitely not the same topological shape as our world, remember, because there are two tours that cannot be shrunk to a point, and because there are tours that don't divide the torus in two. However, the inside of a sphere is the exact same thing, topologically, as the outside—mathematicians have found ways to turn spheres inside out.
Time Travel and Paradoxes
Some people hypothesize that time travel is impossible because we haven't seen any evidence of it. Now, absence of evidence is not evidence of absence, but time travel does have its problems. A lot of these come down to paradoxes—apparent contradictions. Many of these paradoxes follow a particular pattern:
1. Time travel into the past.
2. Change things in the past.
3. Prevent yourself from being born.
4. Prevent step 1 from happening (because if you're not born, you can't time travel into the past).
Rather grimly, one of the canonical examples of a time travel paradox is the grandfather paradox, where step 2 in the preceding pattern involves killing your grandfather. You absolutely don't need to share this with your students. A friendlier example comes from Back to the Future, in which Marty McFly accidentally prevents his mother from falling in love with his father, and he needs to fix the situation to ensure he'll be born.
Scientists and the like have hypothesized many ways to resolve these paradoxes, including parallel universes.
Time Travel and Relativity
Think about yourself standing, and think about what it's like for someone to zoom past you on a bike. That person seems fast. But if you're biking alongside the other person, she suddenly doesn't seem so fast, right?
So speed is relative, and it is for everything in the universe except one thing: light (generally speaking—this also includes other kinds of electromagnetic radiation). So, no matter how fast you go, light always goes at the ultimate speed, about 186,000 miles per second.
The consequences of speed's relativity are really, really cool. When you work out the math, you find that the faster you go, the slower time goes for you relative to anyone else who isn't moving very fast. The thing is, you have to be going very, very fast for time to slow down a lot. So far, experiments we've done have only been able to have fast clocks run fractions of a second slower than stationary clocks.
What does this mean for time travel? Some think that we can get time to slow down so much that it goes backward—the problem is, it means we have to figure out how to go faster than light.
Click the link below to download the handouts for this lesson plan.
